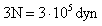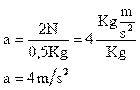Segunda ley de Newton o ley fundamental de la dinámica

La segunda ley de Newton expresa que:

Mutationem motus proportionalem esse vi motrici impressæ, & fieri secundum lineam rectam qua vis illa imprimitur.¹¹​

Esta ley se encarga de cuantificar el concepto de fuerza. La aceleración que adquiere un cuerpo es proporcional a la fuerza neta aplicada sobre el mismo. La constante de proporcionalidad es la masa del cuerpo (que puede ser o no ser constante). Entender la fuerza como la causa del cambio de movimiento y la proporcionalidad entre la fuerza impresa y el cambio de la velocidad de un cuerpo es la esencia de esta segunda ley.¹⁴​

Si la masa es constante

Si la masa del cuerpo es constante se puede establecer la siguiente relación, que constituye la ecuación fundamental de la dinámica:

{ F_resultante=ma

Donde m es la masa del cuerpo la cual debe ser constante para ser expresada de tal forma. La fuerza neta que actúa sobre un cuerpo, también llamada fuerza resultante, es el vector suma de todas las fuerzas que sobre él actúan. Así pues:¹⁵​

{ ∑F=ma

• La aceleración que adquiere un cuerpo es proporcional a la fuerza aplicada, y la constante de proporcionalidad es la masa del cuerpo.
• Si actúan varias fuerzas, esta ecuación se refiere a la fuerza resultante, suma vectorial de todas ellas.
• Esta es una ecuación vectorial, luego se debe cumplir componente a componente.
• En ocasiones será útil recordar el concepto de componentes intrínsecas: si la trayectoria no es rectilínea es porque hay una aceleración normal, luego habrá también una fuerza normal (en dirección perpendicular a la trayectoria); si el módulo de la velocidad varía es porque hay una aceleración en la dirección de la velocidad (en la misma dirección de la trayectoria).
• La fuerza y la aceleración son vectores paralelos, pero esto no significa que el vector velocidad sea paralelo a la fuerza. Es decir, la trayectoria no tiene por qué ser tangente a la fuerza aplicada (sólo ocurre si al menos, la dirección de la velocidad es constante).
• Esta ecuación debe cumplirse para todos los cuerpos. Cuando analicemos un problema con varios cuerpos y diferentes fuerzas aplicadas sobre ellos, deberemos entonces tener en cuenta las fuerzas que actúan sobre cada uno de ellos y el principio de superposición de fuerzas. Aplicaremos la segunda ley de Newton para cada uno de ellos, teniendo en cuenta las interacciones mutuas y obteniendo la fuerza resultante sobre cada uno de ellos.

Representación del sumatorio de las fuerzas. Aquí se está sumando dos veces la fuerza No. 2. La resultante (marcada con rojo) responde a la siguiente ecuación: :{ F_resultante=F₁+2⋅F₂+F₃

El principio de superposición establece que si varias fuerzas actúan igual o simultáneamente sobre un cuerpo, la fuerza resultante es igual a la suma vectorial de las fuerzas que actúan independientemente sobre el cuerpo (regla del paralelogramo). Este principio aparece incluido en los Principia de Newton como Corolario 1, después de la tercera ley, pero es requisito indispensable para la comprensión y aplicación de las leyes, así como para la caracterización vectorial de las fuerzas.¹⁴​ La fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. Las fuerzas son causas que producen aceleraciones en los cuerpos. Por lo tanto existe una relación causa-efecto entre la fuerza aplicada y la aceleración que este cuerpo experimenta.

De esta ecuación se obtiene la unidad de medida de la fuerza en el Sistema Internacional de Unidades, el Newton:

{ 1 hinspN=1 hinsp{{kg⋅m} hinsp/s^2}

Por otra parte, si la fuerza resultante que actúa sobre una partícula no es cero, esta partícula tendrá una aceleración proporcional a la magnitud de la resultante y en dirección de esta (debido a que la masa siempre es un escalar positivo). La expresión anterior así establecida es válida tanto para la mecánica clásica como para la mecánica relativista.

Si la masa no es constante

Si la masa de los cuerpos varía, como por ejemplo un cohete que va quemando combustible, no es válida la relación { F=ma y hay que hacer genérica la ley para que incluya el caso de sistemas en los que pueda variar la masa. Para ello primero hay que definir una magnitud física nueva, la cantidad de movimiento, que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:

{ p=mv

Newton enunció su ley de una forma más general:

{ F_neta={ d(mv) dt

De esta forma se puede relacionar la fuerza con la aceleración y con la masa, sin importar que esta sea o no sea constante. Cuando la masa es constante sale de la derivada con lo que queda la expresión:

{ F_neta=m,{ dv dt

Y se obtiene la expresión clásica de la Segunda Ley de Newton:

{ F_neta=ma

La fuerza, por lo tanto, es un concepto matemático el cual, por definición, es igual a la derivada con respecto al tiempo del momento de una partícula dada, cuyo valor a su vez depende de su interacción con otras partículas. Por consiguiente, se puede considerar la fuerza como la expresión de una interacción. Otra consecuencia de expresar la Segunda Ley de Newton usando la cantidad de movimiento es lo que se conoce como principio de conservación de la cantidad de movimiento: si la fuerza total que actúa sobre un cuerpo es cero, la Segunda ley de Newton nos dice que

0={ dp dt

Es decir, la derivada de la cantidad de movimiento con respecto al tiempo es cero en sus tres componentes. Esto significa que la cantidad de movimiento debe ser constante en el tiempo en módulo dirección y sentido (la derivada de un vector constante es cero).¹⁶​

La segunda ley de Newton solo es válida en sistemas de referencia inerciales pero incluso si el sistema de referencia es no inercial, se puede utilizar la misma ecuación incluyendo las fuerzas ficticias (o fuerzas inerciales). Unidades y dimensiones de la fuerza:

• Unidades S.I.: {\displaystyle {\rm {Newton={kg\cdot m \over s^{2}}}}}
• Sistema cegesimal: dina
• Equivalencia: 1 N= {\displaystyle 10^{5}} dinas

Cantidad de movimiento o momento lineal[editar]

En el lenguaje moderno la cantidad de movimiento o momento lineal de un objeto se define mediante la expresión {\displaystyle \mathbf {p} ={m\mathbf {v} }} . Es decir, es una magnitud vectorial proporcional a la masa y a la velocidad del objeto. Partiendo de esta definición y aplicando la ley fundamental de la mecánica de Newton, las variaciones de la cantidad de movimiento se expresan en función de la fuerza resultante y el intervalo de tiempo durante el cual se ejerce esta:

{\displaystyle \mathbf {F} =m\mathbf {a} =m\,{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}}

{\displaystyle \mathbf {F} \,\mathrm {d} t=m\mathrm {d} \mathbf {v} ={\mathrm {d} (m\mathbf {v} )}=\mathrm {d} \mathbf {p} }

Tomando el intervalo de tiempo de t₁ a t₂ e integrando se obtiene

{\displaystyle \mathbf {I} =\int _{t_{1}}^{t_{2}}\mathbf {F} \,\mathrm {d} t=\int _{p_{1}}^{p_{2}}\mathrm {d} \mathbf {p} =\mathbf {p} _{2}-\mathbf {p} _{1}=\Delta \mathbf {p} }

Al vector I se le denomina impulso lineal y representa una magnitud física que se manifiesta especialmente en las acciones rápidas o impactos, tales como choques, llevando módulo dirección y sentido. En este tipo de acciones conviene considerar la duración del impacto y la fuerza ejercida durante el mismo.

De la expresión obtenida se deduce que el impulso lineal es igual a la variación de la cantidad de movimiento. Si la fuerza resultante es cero (es decir, si no se actúa sobre el objeto) el impulso también es cero y la cantidad de movimiento permanece constante. Llamamos a esta afirmación ley de conservación del impulso lineal, aplicada a un objeto o una partícula.¹⁷​

Sus unidades en el Sistema Internacional son {\displaystyle {\rm {kg\cdot {\tfrac {m}{s}}}}}

Conservación de la cantidad de movimiento

Bolas representando choque elástico

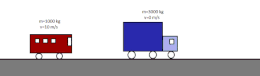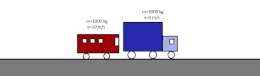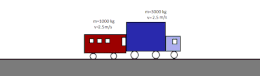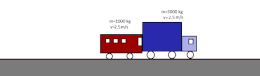
• Choque elástico: permanecen constantes la cantidad de movimiento y la energía cinética. Dos partículas de masas diferentes que solo interactúan entre sí y que se mueven con velocidades constantes y distintas una hacia la otra. Tras el choque, permanece constante la cantidad de movimiento y la energía cinética.

Coches representando choque inelástico

• Choque inelástico: permanece constante la cantidad de movimiento y varía la energía cinética. Como consecuencia, los cuerpos que colisionan pueden sufrir deformaciones y aumento de su temperatura. Tras un choque totalmente inelástico, ambos cuerpos tienen la misma velocidad. La suma de sus energías cinéticas es menor que la inicial porque una parte de esta se ha transformado en energía interna; en la mayoría de los casos llega a ser disipada en forma de calor debido al calentamiento producido en el choque. En el caso ideal de un choque perfectamente inelástico entre objetos macroscópicos, estos permanecen unidos entre sí tras la colisión.¹⁸​

Aplicaciones de la segunda ley de Newton[editar]

Entre las posibles aplicaciones de la Segunda Ley de Newton, se pueden destacar:

• Caída libre: es un movimiento que se observa cuando un objeto se deja caer desde una cierta altura sobre la superficie de la tierra. Para estudiar el movimiento se elige un sistema de coordenadas donde el origen del eje y está sobre esta última. En este sistema tanto la velocidad de caída como la aceleración de la gravedad tienen signo negativo. En el ejemplo representado, se supone que el objeto se deja caer desde el reposo, pero es posible que caiga desde una velocidad inicial distinta de cero.¹⁸​

Péndulo Simple: Diagrama de Fuerzas

• Péndulo simple: partícula de masa m suspendida del punto O por un hilo inextensible de longitud ly de masa despreciable. Si la partícula se desplaza a una posición θ₀ (ángulo que hace el hilo con la vertical) y luego se suelta, el péndulo comienza a oscilar. El péndulodescribe una trayectoria circular, un arco de una circunferencia de radio l. Las fuerzas que actúan sobre la partícula de masa m son dos, el peso y la tensión T del hilo.

Si se aplica la segunda ley, en la dirección radial:

{\displaystyle m\cdot a_{n}=T-mg\cdot \cos {\theta }}

donde a_n representa la aceleración normal a la trayectoria. Conocido el valor de la velocidad v en la posición angular se puede determinar la tensión T del hilo. Esta es máxima cuando el péndulo pasa por la posición de equilibrio

{\displaystyle T=mg+{{m\cdot v^{2}} \over {\ell }}} ,

donde el segundo término representa la fuerza centrífuga.

Y la tensión es mínima, en los extremos de su trayectoria, cuando la velocidad es cero

{\displaystyle T=mg\cdot \cos {\theta }}

en la dirección tangencial:

{\displaystyle m\cdot a_{t}=-mg\cdot \operatorname {sen} {\theta }}

2.b) Segunda Ley de Newton o Ley de fuerza

La Segunda Ley de Newton, también conocida como Ley Fundamental de la Dinámica, es la que determina una relación proporcional entre fuerza y variación de la cantidad de movimiento o momento lineal de un cuerpo. Dicho de otra forma, la fuerza es directamente proporcional a la masa y a la aceleración de un cuerpo.

Cuando Newton unificó la fuerza de gravedad terrestre, incluida en su segunda ley o Ley de Fuerza, con la fuerza de gravedad de las órbitas planetarias en su Ley de Gravitación Universaltenía sentido el principio de igualdad entre masa inercial y gravitatoria citado, pues así lo indicaban todos los experimentos científicos y fenómenos naturales.

Fuerza / masa = aceleración
F = m a

Además, la Física Clásicade Newton asumía que una fuerza constante podría acelerar una masa hasta el infinito.

La Segunda Ley de Newtonha sido modificada por la Teoría de la Relatividad Especial de Einstein al recoger el fenómeno de aumento de la masa de un cuerpo con la velocidad y, posteriormente, por la Relatividad General al introducir perturbaciones del espacio-tiempo. Una fuerza constante ya no podrá acelerar una masa hasta el infinito; no obstante la relación de proporcionalidad entre masa y fuerza que provoca la aceleración se sigue manteniendo para la masa en un instante concreto.

El primer experimento que confirmaba la masa relativista fue el descubrimiento por Bücherer en 1908 de que la relación de la carga del electrón y su masa (e / m) era menor para electrones rápidos que para los lentos. Posteriormente, incontables experimentos confirman los resultados y fórmulas físicas anteriores.

La masa y la energía se convierten así en dos manifestaciones de la misma cosa. Los principios de conservación de la masa y de la energía de la mecánica clásica pasan a configurar el principio de conservación de la energía-masa relativista más general.

Sin embargo, la Teoría de la Relatividad de Einstein sigue sin decirnos qué es esa cosa que se manifiesta como masa o como energía. Por ello, la idea de incontables experimentos que confirman dicha teoría es un poco aventurada, una cosa es que matemáticamente cuadren algunos resultados y otra que la realidad física subyacente sea la propugnada por la mecánica relativista.

Por el contrario, la Mecánica Global explica la fuerza de la gravedad como el efecto de la tensión de la curvatura longitudinal de la estructura reticular de la materia o éter global, para no confundirlo con el éter clásico o el nuevo éter luminífero. También explica en qué consiste la energía electromagnética y cómo se forma la masa, es decir, ha unificado la gravedad, la energía y la masa.

Por supuesto, como se verá más adelante, a la nueva teoría alternativa también le cuadran los mismos experimentos y resultados con idéntica precisión que los de la mecánica relativista deEinstein. Además, a la Física Global le encajan otros aspectos derivados de la no existencia de las típicas singularidades relativistas y de la compatibilidad entre la teoría del átomo de la Mecánica Global, la Dinámica Global de la escala humana normal y la Astrofísica Global.

Como se ha comentado, el principio de igualdad entre masa inercial y gravitatoria permite encuadrar en la Ley Fundamental de la Dinámica a la fuerza de gravedad de los planetas. La Física Relativistade Einstein mantiene dicho principio, pero se ve obligada a alterar el espacio y el tiempo para cuadrar pequeñas diferencias observadas en la órbita de Mercurio y de los planetas en general. No obstante, dichas diferencias ya habían sido explicadas con la misma fórmula por Paul Gerber con una perspectiva clásica en 1898.

En la nueva perspectiva de la Física Global dicho principio deja de ser necesario; pues con la definición y caracterización de la masa física, el movimiento de la masa sigue las mismas reglas en la estructura reticular de la materia o éter global, con independencia del origen de las fuerzas. Además de la variación de la masa física con la velocidad, la Ley de la Gravedad Global introduce la variación de la fuerza gravitacional con la velocidad para un mismo punto del éter global.

En el nuevo modelo de la Dinámica Global, la Segunda Ley de Newton, Ley de Fuerza o Ley Fundamental de la Dinámica se sigue cumpliendo en cuanto a la relación entre fuerza, masa y aceleración, aunque no es constante.

Cuando la velocidad empieza a ser relevante respecto a la velocidad de la luz, el aumento de masa física se debe al propio mecanismo de conversión entre la fuerza aplicada –provenga de la energía gravitacional o no– y la energía cinética. Ahora bien; el incremento de masa se verá compensado con un incremento de la atracción gravitacional, como en el caso de las órbitas clásicas de los planetas, por lo que este efecto no provocará la precesión anómala del perihelio de Mercurio.

Con independencia del incremento de masa con la velocidad, la fuerza de gravedad se incrementara por ser el doble para la masa cinética – masa equivalente a la energía cinética.

En otras palabras, de las dos componentes de la atractis causa, la debida a la tensión de la curvatura longitudinal del éter global y la debida a la velocidad de los cuerpos con masa respecto al éter global, sólo la segunda será la responsable de la variación adicional de la fuerza gravitacional que causa la precesión anómala de las órbitas de los planetas, respecto a lo previsto por la Ley de Gravitación Universal de Isaac Newton.

Torre de PisaFuerza, masa y aceleración

De acuerdo con la Mecánica Global, la diferencia conceptual se debe a los mecanismos de la interacción del éter global como soporte material directo de la masa y la energía cinética, o como soporte indirecto de la energía electromagnética.

La discusión del concepto de la atractis causa se efectúa en los apartados de la Ley de la Gravitación Universal de Newton y de la Ley de la Gravedad Global del libro sobre esta última ley.

Resumiendo, la Dinámica Global mantiene el igual comportamiento de la masa física en movimiento con o sin fuerzas de gravedad en cuanto a la proporcionalidad entre fuerza, masa y aceleración, siendo necesario realizar las siguientes matizaciones:

• El principio de igualdad entre masa inercial y gravitatoria de Newton y Einstein deja de ser un principio dadas las nuevas características del movimiento de la masa.

• Con la velocidad se produce un aumento de la masa. Aunque con diferencias conceptuales respecto al marco de referencia del movimiento, este efecto es parecido en la mecánica relativista y en la Dinámica Global. Nótese que el incremento de masa relativista debido a la velocidad no afectará ni a la proporcionalidad de la fuerza y la masa global o total ni a la fuerza de gravedad por unidad de masa.

• La precesión anómala de la órbita de los planetas se explica por la Ley de la Gravedad Global, al contener una fuerza adicional de la interacción masa-éter global derivada de la velocidad. En la mecánica relativista de Einstein dicha precesión se justifica con alteraciones del espacio-tiempo.

Desde otra perspectiva, la Segunda Ley de Newton acumulará problemas para su cumplimiento general por la citada característica del éter global como soporte material de la masa y del campo de gravedad, y de ser dicho campo de gravedad medio soporte de la energía electromagnética o éter luminífero.

De acuerdo con la Dinámica Global, dichos problemas serán derivados de:

• La variación de la posición espacial del éter global.

• La variación de la tensión longitudinal del éter global para un mismo punto espacial.

Se podría intentar resolver los problemas de la Ley Fundamental de la Dinámica o Ley de Fuerzade Newton con una definición de fuerza más general que incluyera los desplazamientos respectivos; pero habrá que tener cuidado pues, además de enmascarar conceptos distintos, podría no existir la proporcionalidad estricta con la masa. Probablemente los desplazamientos derivados de los dos puntos anteriores se pueden reconducir al tratamiento del movimiento de la masa sobre el éter global, por suponer una variación de la velocidad relativa en el sentido de Galileo entre el éter global y la masa.

Es importante recordar que la Física Global además de matizar la Segunda Ley de Newton, lo hace en un contexto en que el movimiento de los cuerpos no se produce en un vacío abstracto sino en la estructura reticular tridimensional de la materia, con su característica simetría radial en un espacio euclidiano.

Finalmente, no veo que la Mecánica Cuántica diga nada en relación a esta Segunda Ley de Newton, excepto que supone una aproximación macroscópica de la realidad debido a su principio de incertidumbre. Aunque, en el ámbito subatómico, tampoco la Mecánica Cuánticasabe muy bien qué es un electrón y sigue buscando explicaciones al denominado efecto túnelo al experimento de doble rendija con fotones, incluso busca la solución en viajes en el tiempo hacia atrás.

La Mecánica Global explica, entre otras muchas cosas, el efecto túnel y el experimento de doble rendija y mantiene que el movimiento orbital de los electrones es consecuencia del movimiento de los puntos de relajación de la tensión gravito-magnética del éter global. La justificación detallada de estas afirmaciones se deduce de la nueva estructura del átomopropuesta en el libro de la Mecánica Global.

descubrimiento

Siempre he asumido/ha dicho que la 2ª ley de Newton es una ley empírica – que debe ser descubierto por el experimento. Si este es el caso, lo que hizo experimentos de Newton hacer para descubrir esto? Está relacionado con sus estudios sobre el movimiento de la luna y de la tierra? Fue capaz de analizar estos datos para ver que las masas fueron inversamente proporcionales a la aceleración, si suponemos que la fuerza de la luna sobre la tierra es igual a la fuerza que la tierra ejerce sobre la luna?

Fuente: https://www.i-ciencias.com/pregunta/1180/como-newton-descubre-su-segunda-ley

caracteristicas

caracteristicas d ela segunda ley de newton

 Segunda Ley de Newton
La aceleración que un cuerpo adquiere es directamente proporcional a la resultante de las fuerzas que actúan en él, y tiene la misma dirección y el mismo sentido que dicha resultante.
R = m a , o bien, å F = m a.
Consideremos un cuerpo sometido a la acción de varias fuerzas (F1, F2, F3, etc.). Sabemos que al suceder esto, es posible sustituir el sistema de fuerzas por una fuerza única, la resultante R del sistema.
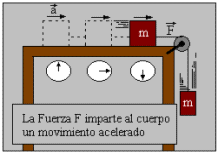La aceleración que el cuerpo vaya a adquirir por la acción del sistema de fuerza, se obtendrá como si el cuerpo estuviese sometido a la acción de una fuerza única, igual a R. La ecuación F = ma será en este caso, sustituida por R = ma, y el vector a tendrá la misma dirección y el mismo sentido que el vector R. La ecuación R = ma es la expresión matemática de la Segunda Ley de Newton en su forma más general.
La Segunda Ley de Newton es una de las leyes básicas de la mecánica, se utiliza en el análisis de los movimientos próximos a la superficie de la tierra y también en el estudio de los cuerpos celestes.
El mismo Newton la aplicó al estudiar los movimientos de los planetas, y el gran éxito logrado constituyó una de las primeras confirmaciones de esta ley.
La masa de un cuerpo es el cociente entre la fuerza que actúa en el mismo, y la aceleración que produce en él, o sea:

m = F / a .

Cuanto mayor sea la masa de un cuerpo, tanto mayor será su inercia; es decir, la masa de un cuerpo es una medida de la inercia del mismo.
LISTA DE MATERIALES EMPLEADOS

Ejercicios Resueltos

Ejemplo de problemas relacionados con la Segunda Ley de Newton.

• 1. Una fuerza le proporciona a la masa de 2,5 Kg. una aceleración de 1,2 m/s2. Calcular la magnitud de dicha fuerza en Newton y dinas.

Datos

m = 2,5 Kg.

a =1,2 m/s2.

F =? (N y dyn)

Solución

Nótese que los datos aparecen en un mismo sistema de unidades (M.K.S.)

Para calcular la fuerza usamos la ecuación de la segunda ley de Newton:

 Sustituyendo valores tenemos:

Como nos piden que lo expresemos en dinas, bastará con multiplicar por 105, luego:

• 2. ¿Qué aceleración adquirirá un cuerpo de 0,5 Kg. cuando sobre él actúa una fuerza de 200000 dinas?

Datos

a =?

m = 2,5 Kg.

F = 200000 dyn

Solución

La masa está dada en M.K.S., en cambio la fuerza está dada en c.g.s.

Para trabajar con M.K.S. debemos transformar la fuerza a la unida M.K.S. de esa magnitud (N)

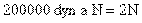
 La ecuación de la segunda ley de Newton viene dada por:

 Despejando a tenemos:

 Sustituyendo sus valores se tiene: